Berechnung der Korrelationen mit Excel
In diesem Beitrag werde ich aufzeigen, wie Sie die Korrelation mit Excel selbst berechnen können. An ein paar Praxisbeispielen werden wir sehen, warum Korrelationen hilfreich sein können.
Für das folgende Praxisbeispiel habe ich mir die Tageskurse einiger ETF’s sowie der Aktie Nestlé bei der SIX abgeholt. Auf Grund des UBS-ETF MSCI JAPAN (FDJPHU/ LU0136240974) hat mich noch die Korrelation zum Währungskurs JPY/CHF interessiert.
| Wertpapier/Währung | Standardabweichung 250 Tage |
| ZKB SILVER ETF (ZSIL/ CH0029792717) | 49.63% |
| ZKB GOLD ETF (ZGLD/ CH0024391002) | 28.84% |
| Xmtch (CH) SLI (XMSLI/ CH0031768937) | 38.36% |
| UBS-ETF MSCI JAPAN (FDJPHU/ LU0136240974) | 46.07% |
| NESTLE N (NESN/ CH0038863350) | 30.42% |
| DB X‑TR DAX (XDAX/ LU0274211480) | 47.06% |
| DB X‑TR SHORT DAX (XSDX/ LU0292106241) | 36.93% |
| JPY/CHF | 17.13% |
Die meisten dieser Wertpapiere bzw. Währungskurs stehen in Zusammenhang mit meinem Portfolio, zudem wollte ich meine gefühlsmässigen Annahmen bezüglich Korrelationen zwischen den Wertpapieren überprüfen.
Korrelationen auf Tageskursen
Ich habe die Korrelationen für ein Jahr bzw. für 90-Tage auf den Tageskursen berechnet.
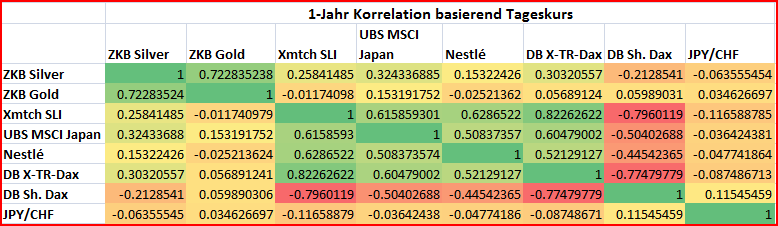
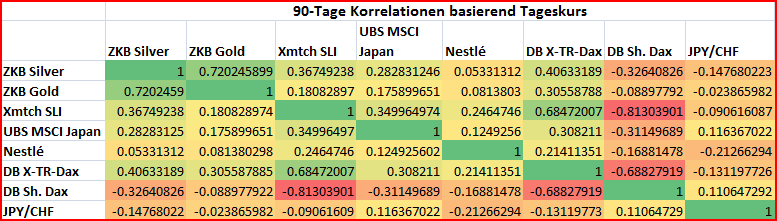
Die 90-Tage-Korrelationen wurden vom 22.04.2009 — 28.08.2009 berechnet, es sind also nicht 3 Monate, sondern 90 Handelstage. Samstag, Sonntag und Feiertage gibt es keinen Börsenhandel, daher sind diese Tage auch nicht in die Berechnung eingeflossen.
Korrelationen auf Wochenkurse
Ab einem Zeitraum von 6 Monaten empfehle ich, die Wochenkurse zu nehmen und nicht die Tageskurse. Daher habe ich auch die Jahreskorrelationen auf der Basis von Wochenkursen berechnet, wobei ich den Freitag als Kurstag benutzte. Im Dezember 2008 und Mai 2009 gibt es einen Zwei-Wochen-Sprung, dies sollte das Ergebnis aber nicht stark beinträchtigen.
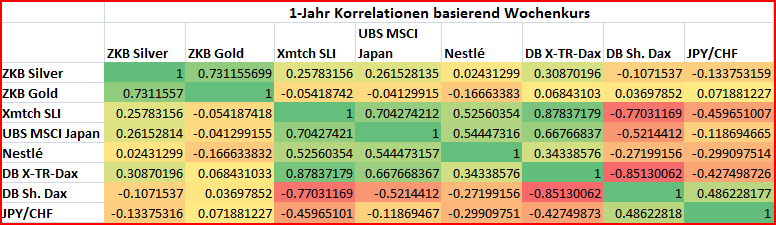
Tageskursen können manchmal Extreme ausweisen, was das Resultat der Korrelationen ein wenig verfälscht. Diese Extreme könnten sich innerhalb einer Woche wieder normalisieren und daher sind Wochenkurse für die Erstellung von Korrelationen über einen längeren Zeitraum oftmals die bessere Wahl.
Korrelationen in der Praxis und meine gefühlsmässigen Annahmen
Wer die Kurse täglich oder wöchentlich beobachtet, wird wahrscheinlich automatisch gewisse Korrelationen zwischen den Kursen der Wertpapiere feststellen. Beispielsweise steigt der Ölpreis zurzeit mit den Aktienindizes, dies ist nicht immer so. Noch im Jahr 2008, als der Ölpreis über UDS 100 lag, wiesen diese beiden Assets eine negative Korrelation auf. Ich werde im Folgenden auf einige Korrelationen die mein Portfolio beeinflussen eingehen.
Silber, Gold und Aktien
Es gibt eine starke Korrelation (>0.7) zwischen Gold und Silber. Ich hatte aber in der letzten Zeit (90 Tage) das Gefühl, das der Silberpreis zunehmend auch mit den Aktienindizes korreliert. Die 90-Tage-Korrelation scheint dies mit dem SLI und dem Dax zu bestätigen. Die auf ein Jahr hochgerechnete Volatilität des Silbers war mit fast 50% weitaus höher als die des Goldes mit nur zirka 29%.
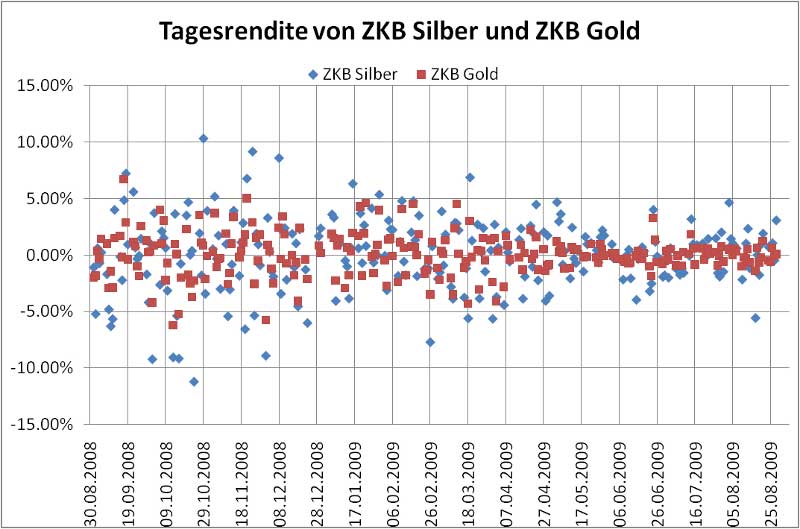
Dass die Streuung beim Silber höher ist, lässt sich hervorragend mit einem Punktdiagramm darstellen. Im Oktober 2008 gab es beim Silber gar eine positive wie negative Rendite in Bereich von 10%.
Silber wird mehr als Gold in der Industrieproduktion verwendet, daher scheinen die höhere Korrelation zu den Aktien und höhere Volatilität gegenüber Gold nicht zu erstaunen.
Nestlé, SLI und Dax
Ich habe zurzeit keinen direkten Aktientitel in meinem Portfolio, vor Kurzem habe ich mit Intel meine letzte Position verkauft. Trotzdem finde ich Nestlé eine mögliche Option für mein Portfolio, er ist mit einer Standardabweichung von zirka 30% weniger volatil als der SLI mit circa 38%. Zudem zahlte Nestlé am 29.04.2009 eine Jahresdividende von CHF 1.40 pro Einheit, d.h. mehr als 3%. Die 90-Tage-Korrelation von Nestlé zum SLI beträgt nur 0.24, was diesen Titel nebst der Dividendenzahlung zusätzlich interessant macht. Dieser Titel könnte definitiv auch eine Bereicherung für ein reines Anleihenportfolio sein.
UBS-ETF MSCI JAPAN und JPY/CHF
Zurzeit habe ich noch den UBS-ETF MSCI JAPAN (FDJPHU/ LU0136240974) in meinem Portfolio. Ich werde das Gefühl nicht los, das der steigende MSCI Japan einhergeht mit fallendem Yen. Meine Annahme wird nur teilweise von der 1‑Jahr-Wochenkurs-Korrelation bestätigt.
DB X‑TR DAX Dax und DB X‑TR DAX Short Dax
Wahrscheinlich erwarten Sie zwischen den beiden ETF’s eine vollständige inverse Korrelation. Die 1‑Jahr-Wochenkurs-Korrelation kommt mit ‑0.85 der ‑1 noch am nächsten. Ich stelle mir vor, dass die Abweichung auf Grund des fehlenden Volumens an der SIX zu Stande kommt bzw. die beiden ETF’s den Dax kaum synchron exakt tracken. Diese Theorie wird durch die 1‑Jahr-Wochenkurs-Korrelation gestützt, damit werden die täglichen Abweichungen zum Net Asset Value (NAV) teilweise “geglättet”.
Anmerkung zu Excel
Damit die folgenden Arbeitsmappen korrekt funktionieren, müssen Sie die Ausführung von Makros erlauben. Zuerst können Sie diese ohne die Ausführung der Makros laden und den Quellencode der Makros im Microsoft Visual Basic [ALT]+[F11] prüfen. Wie Sie oben sehen, wurde Excel 2007 mit der “Bedingten Formatierung” erweitert. Eine solche Einfärbung einer Matrix ist nun “kinderleicht”.
Funktionen
KORREL(Matrix1;Matrix2)
Gibt den Korrelationskoeffizient einer zweidimensionalen Zufallsgrösse zurück, deren Werte in den Zellbereichen Matrix1 und Matrix2 stehen. Das Excelmakro CorrMatrix(Matrix) erleichtert die Berechnung einer Matrix von Korrelationen, siehe “Computing The Correlation Matrix – By Simon Benninga”. Dort können Sie auch entnehmen, wie eine solche Funktion in Excel eingegeben wird.
KOVAR(Matrix;Matrix2)
Diese Funktion gibt die Kovarianz zurück, den Mittelwert der für alle Datenpunktpaare gebildeten Produkte der Abweichungen. Wie beim Korrelationskoeffizienten steht eine positive Kovarianz für eine positive lineare Assoziation zwischen den Datenpunktpaar und umgekehrt. Da der Wert der Kovarianz von den Einheiten der Datenpunktpaare abhängt, gibt es keinen “absoluten” Wert. Für den Anwender ist der Korrelationskoeffizient für die Beurteilung der Stärke der Assoziation weitaus besser geeignet. Das Excelmakro VarCovar(Matrix) ermöglicht die Berechnung einer Matrix von Kovarianzen.
Arbeitsmappe für Excel 2007: Korr_Beispiel.xlsm 2007
Arbeitsmappe: Korr_Beispiel.xls
Pingback: Ist die Buy-und-Hold-Strategie noch zeitgemäss? » Grafioschtrader Investment Blog