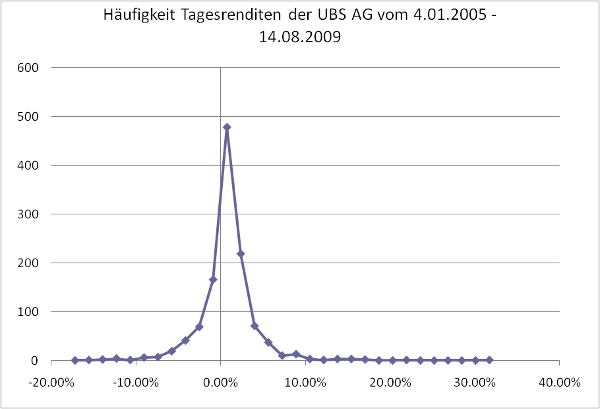
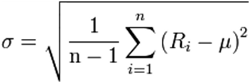Vielleicht haben Sie auch einen Kollegen/in die Ihnen erzählt, sie habe gerade “viel” Geld mit UBS-Aktien gemacht. Vielleicht hat diese Person nur gerade Aktien von 3 Unternehmen und behauptet, sie habe den grossen Durchblick bei Investitionen. Mit Simulationen kann einfach aufgezeigt werden, dass wenig diversifizierte Portfolios fast in 70% aller Fälle hinter der Performance von gut diversifizierten Portfolios zurückbleiben.
Ich werde daher einige Einträge in diesem Blog der Portfoliodiversifikation widmen, dazu müssen zuerst ein wenig Wissen bezüglich Volatilität, Korrelationen usw. vermittelt werden. Natürlich ist dies nicht für alle interessant und zudem muss man dabei sein Gehirn ein bisschen bemühen. Viele Kleinanleger bewegen sich zufrieden auf dem seichten Niveau der TV-Sendungen SF Börse. Gerade die Sendung SF Börse bewegt sich auf tiefem Niveau. Hierzu ein Beispiel: Oftmals gegen die bei der Bekanntgabe von Unternehmensquartalszahlen dessen Aktienkurs nach unten, daraus schliesst SF Börse, das die Anleger bessere Zahlen erwartet haben. Dabei geht vergessen, dass der Aktienkurs dieses Unternehmens vielleicht schon wenige Tage vorher in der Erwartung besserer Quartalszahlen “zu” stark gestiegen war. Wahrscheinlich kennt SF Börse die Börsenweisheit nicht: “Kaufe das Gerücht, verkaufe die Nachricht”. Anderseits ist es nicht erstaunlich das solche Privatanleger im Jahre 2008 mehr als 40% ihres Vermögens an der Börse verspekuliert haben.
Es ist relativ leicht, die oben genannte Angeber/in zu entzaubern. Schon nur die Frage nach dem quantitativen eingegangenen Risiko wird sie wahrscheinlich nicht beantworten können. Es ist dämlich nur von Renditen zu sprechen, ohne dabei auch die damit verbundenen Risiken zu erwähnen.
Risiko an realen Aktien bzw. ETF
Gerade viele Schweizer Privatanleger spekulieren mit UBS Aktien, dabei geht die hohe Volatilität dieser Aktie vergessen. Scheinbar zieht die viele Medienpräsenz der UBS die kleinen Privatanleger an. Manchmal kommt bei mir das Gefühl auf, der gesamte Bundesrat arbeite nur noch an den Problemen der UBS und die Schweizer Regierung sei der UBS hörig.
Dieser Tabelle vom 14.08.2009 kann entnommen werden, dass die Volatilität bei der UBS-Aktie weitaus am höchsten ist. Nur die Rendite der letzten 30 Tage belohnt dieses eingegangene Risiko. Wer schon viel Risiko eingehen will, hätte besser die Credit-Suisse gewählt, die Investition in UBS-Aktien war das Auslassen dieser viel besseren Opportunität. Weniger riskant wäre die Investition in den DB X‑Trackers DJ Stoxx 600 Banks ETF als eine Direktinvestition in einen einzelnen Banktitel. Wobei bei diesem ETF das Währungsrisiko noch berücksichtigt werden müsste und der Total Expense Ratio (TER) 0.3% beträgt.
Auch in diesem volatilen Marktumfeld bleibt das Risiko einer Nestlé Aktie gegenüber den Banktiteln in einem bescheidenen Rahmen.
Herkunft der historischen Daten
Bei OnVista kann unter der Rubrik Techn.-Analyse->Kennzahlen die Volatilität in % für die letzten 30 bzw. 250 Tage eingesehen werden, wobei mit 250 Tagen ein Handelsjahr abgedeckt wird. Weitere freie Quellen für historische Kurse von Schweizer Titeln:
Tabellenkalkulationsprogramm
Wahrscheinlich kennen viele Leser dieses Blogs das Tabellenkalkulationsprogramm Microsoft Excel oder OpenOffice Calc. Ich werde meine Berechnungen soweit als möglich mit diesen Programmen durchführen und die Arbeitsmappen bereitstellen.
Risiko und Volatilität
Volatilität wird in der Finanzwelt als eine der bedeutendsten Risikokennzahlen angesehen. Allerdings ist diese Risikokennziffer ein zweischneidiges Schwert. Gehen wir beispielsweise von einem simplen Aktieninvestment aus, so gibt Volatilität keine Auskunft darüber, ob die Aktie steigen oder fallen wird. Vielmehr bedeutet eine gestiegene Volatilität zum einen, dass die Wahrscheinlichkeit von grossen Kursverlusten gestiegen ist, zum anderen aber auch, dass es wahrscheinlicher geworden ist, dass die Aktie starke Kursgewinne verzeichnen wird. Demzufolge ist es nun weniger wahrscheinlich, dass die Aktie dicht um das aktuelle Niveau schwankt. Volatilität ist ein Mass für die Schwankungsintensität eines Aktienkurses, die häufig als die annualisierte Standardabweichung der Tagesrenditen dargestellt wird. [1]
Fast alle Fonds-Ratingagenturen listen die Standardabweichung in ihren Berichten auf. Normalerweise werden die Standardabweichungen der letzten drei, fünf und zehn Jahre aufgeführt. Wenn es nur Zahlen für ein oder zwei Jahre gibt, kann die Standardabweichung auf Grund der vierteljährlichen Renditen mit 2 (√4) bzw. der monatlichen Renditen mit 3.46 (√12) multipliziert werden. Die Standardabweichungen verschiedener Asset-Klassen sehen in der Regel so aus:
Immer wenn Ihnen Ihr Bankberater versucht eine bestimmte Investition schmackhaft zu machen, fragen Sie ihn nach der Standardabweichung oder einem anderen üblichen Risikomass. Lassen Sie sich dieses Risikomass ausführlich erklären, wenn der Berater dies nicht kann, so sollten Sie diesen umgehend durch eine kompetentere Person ersetzen. Bei der Standardabweichung sollten Ihrem Berater die folgenden Aussagen bekannt sein.
In der Mathematik wird die Standardabweichung einer Zufallsvariablen häufig mit dem griechischen Buchstaben σ (Sigma) bezeichnet und ist in der Regel wie folgt definiert:
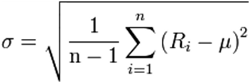
Ri: Rendite mit Anzahl i; n: Periodenanzahl; x: Anlagebeginn; y: Anlageende
Bei Wikipedia können Sie die Formel anhand eines Beispieles in Aktion sehen. Wichtig ist die sind die Häufigkeiten der Realisationen in den verschiedenen Intervallen:
- 68.27% aller Realisationen haben eine Abweichung von höchstens einer Standardabweichung vom Mittelwert.
- 95.45% aller Realisationen haben eine Abweichung von höchstens 2 Standardabweichungen vom Mittelwert.
- 99.73% aller Realisationen haben eine Abweichung von höchstens 3 Standardabweichungen vom Mittelwert.
Volatilität bei Jahresrenditen anhand eines Beispieles
Arbeitsmappe: UbsStandardAbweichungRendite.xls
Ich habe auf Grund der Jahresrenditen der UBS-Aktie, die Standardabweichungen der letzten 8 Jahre (2000–2008) pro Jahr berechnet. Natürlich kann die Standardabweichung, die nur auf wenigen Werten berechnet wurde, nicht aussagekräftige Resultate für die ersten Jahre liefern. In beiden Finanzkrisenjahren 2007 und 2008 sind Erwartungen und Realität vollständig auseinander gelaufen. Noch bis Ende 2006 war die Standardabweichung um die 17% über Jahre hinweg sehr stabil, erst der Verlust im 2007 liess die Standardabweichung über 21% ansteigen. Die immense Kurseinbusse von über 68% im Jahre 2008 sollte gemäss logarithmierten Normalverteilung nur alle 740 (es ist weit mehr als 3 Standardabweichungen, daher auch mehr als 740 Jahre — aber so genau wollen wir es auch nicht wissen) Jahre möglich sein, das zeigt die Grenzen dieses statistischen Modells für Aktienkurse.
Die Spalte “Intervall 68.27” bedeutet das nur alle 6.3 Jahre ein Verlust bzw. Gewinn von mehr als das im angegeben Intervalls zu rechnen ist. Beispielsweise bewegt sich das Jahr 2006 bei einem Gewinn von 18.92% im erwarteten Intervall [-9.49%, 25.95%].
Die Spalte “Intervall 95.45” bedeutet das nur alle 44 Jahre ein Verlust bzw. Gewinn von mehr als das im angegeben Intervalls zu rechnen ist. Das Jahr 2005 endet im diesem Intervall [-29.18%, 39.33%].
Die Spalte “Intervall 99.73* bedeutet, dass nur all 740 Jahre ein Verlust bzw. Gewinn von mehr als das im angegeben Intervalls zu erwarten ist. Der Verlust von 29% in Jahre 2007 bewegt sich in diesem Intervall [-40.80%, 59.53%].
Korrelationen
Wird ein Vermögen auf verschiedene Asset-Klassen verteilt, hängt das Risiko des Portfolios weniger von der Volatilität der einzelnen Anlage als vom Zusammenhang zwischen den verschiedenen Asset-Klassen ab. Mit der Diversifikation wird versucht, bei einem vorgegebenen Risiko die maximale Rendite zu erzielen, bzw. für eine anvisierte Rendite das geringstmögliche Risiko einzugehen.
Die gegenseitige Abhängigkeit von zwei Anlageformen wird mit dem statistischen Mass der Korrelation gemessen. Dieses Mass liegt definitionsgemäss zwischen +1 und ‑1, wobei eine Korrelation von 1 bedeutet, dass die Renditen zweier Anlagen in einem perfekt positiven Zusammenhang stehen. Eine solche Kombination von Anlagen bietet keine Diversifikation. Ein Korrelationskoeffizient von ‑1 heisst, dass sich die beiden Anlagen genau gegenläufig entwickeln.
Investoren müssen akzeptieren, dass Korrelationen nicht in Stein gemeisselt sind, dies kann der folgenden Tabelle entnommen werden. Hier sind die Jahres-Korrelationen von 1973 bis 2008 einiger Assetklassen zum S&P 500 aufgeführt.
Gerade wenn die Märkte sich in “Stresssituationen” befinden, tendieren die Korrelationen gegen die 1, d.h. alle Asset-Klassen tauchen beispielsweise zusammen ab.
Bei Goldman Sachs kann eine Korrelationsmatrix eingesehen werden.
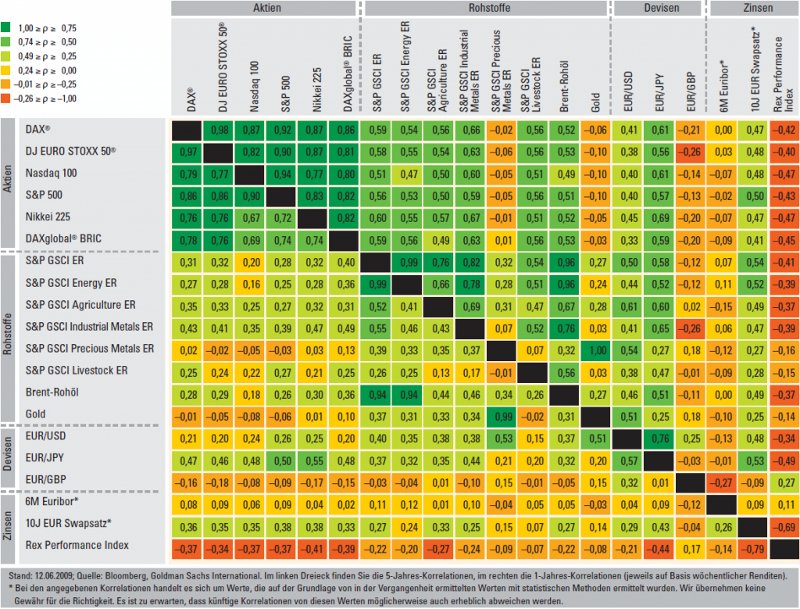
Quelle: Goldman Sachs — Korrelationsmatrix, Juni 2009
Diese Matrix zeigt die Korrelationen der Renditen von verschiedenen Anlageklassen. Dabei sind im linken Dreieck (unterhalb der schwarzen Linie) die Fünfjahreskorrelationen dargestellt. Im rechten Dreieck befinden sich die Einjahreskorrelationen.
Bei der Asset-Klasse Aktien haben die Indizes eine hohe Korrelation zueinander. Bei einigen Rohstoffen Indizes ist die Korrelation seit einem Jahr deutlich höher als bei den Fünfjahreskorrelationen, wobei Gold oder der S&P GSCI Precious Metals ER (Edelmetall) eine gute Diversifikation zu Aktien ist. Staatsanleihen haben gegenüber den Aktien gar eine negative Korrelation. Auf die Spekulation mit Devisen möchte ich hier nicht weiter eingehen.
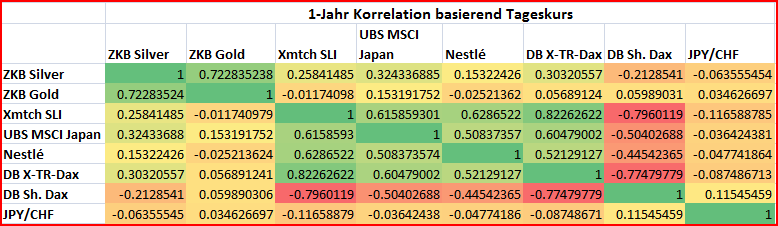
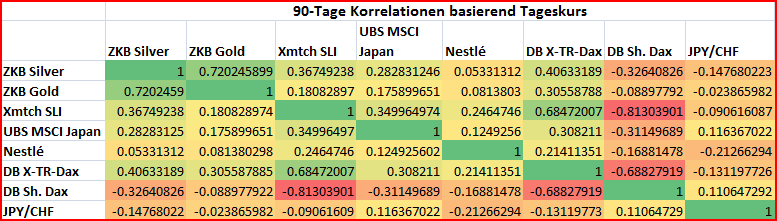
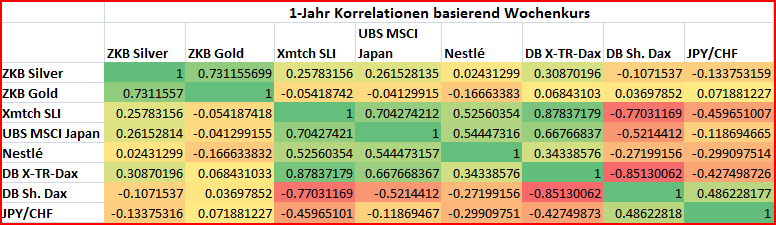
Im Payoff magazine vom 07/2009 habe ich eine weitere Korrelationsmatrix gefunden. Dabei entsprechen alle Werte im linken unteren Dreieck der Korrelation der letzten 52 Wochen (auf wöchentlicher Basis gemessen).
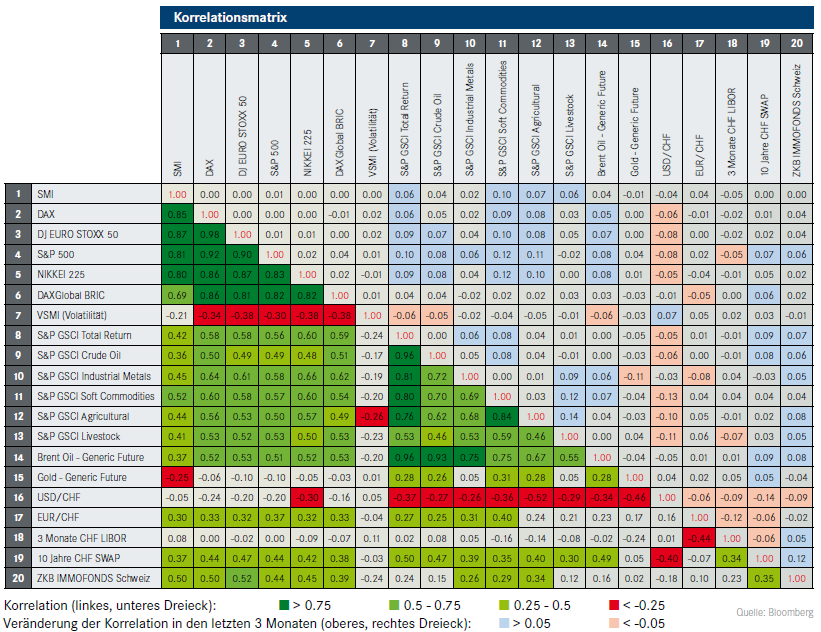
Der USD/CHF Wechselkurs und der Goldpreis weisen eine negative Korrelation von ‑0.46 auf, d.h. wenn der USD gegenüber den CHF schwächer wird, dann steigt der Goldpreis. Mit Gold kann daher der USD teilweise abgesichert werden.
Anmerkung Korrelationen
Auch wenn eine vollständige Korrelation zwischen zwei Titeln besteht, kann die Rendite unterschiedlich hoch ausfallen. Im folgenden Beispiel wurde die Rendite von Grafiosch aus der Rendite von ABC AG multipliziert mit 0.5 + 3% berechnet. Weil die zwei Renditen linear sind, ergibt dies eine vollständige Korrelation.
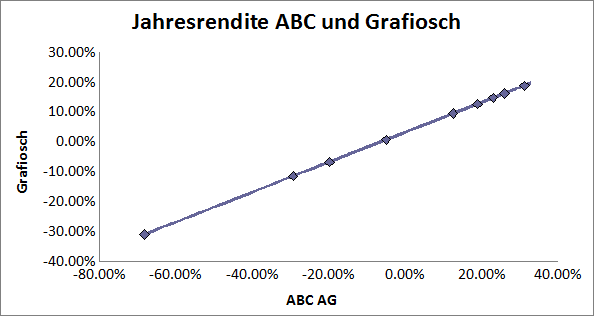
Arbeitsmappe: GrafioschABCLinearKorr.xls
Diversifikation
Auch ein reines Aktienportfolio sollte breit diversifiziert sein. Modellrechnungen haben ergeben, dass ein globales diversifiziertes Portfolio über 100 verschiedene Titel enthalten müsste. Bei einem regionalen Portfolio genügen oft schon 20 Titel. Daraus wird ersichtlich, dass die meisten Privatanleger für eine breite Diversifikation ihres Portfolios gar nicht einzelne Aktientitel kaufen sollten, die Transaktionskosten und der Aufwand wären viel zu hoch. Mit den beiden ETF auf dem MSCI World und dem MSCI Emerging Markets hat der Privatanleger eine günstige Möglichkeit sein Aktienportfolio zu diversifizieren.
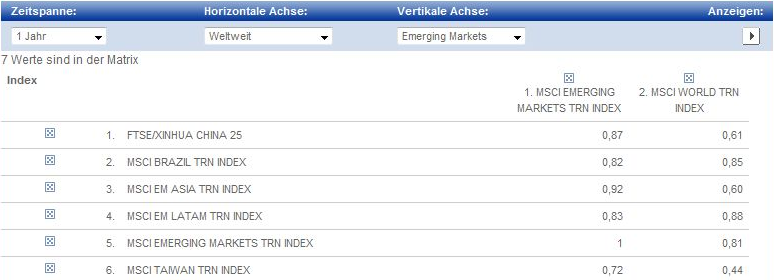
Diese Korrelation können bei db x‑trackers unter Tools–>Korrelationsmatrix für 1, 3 und 5 Jahre eingesehen werden. Die Korrelation zwischen dem MSCI EMERGING MARKETS TRN INDEX und dem MSCI WORLD TRN INDEX ist mit 0.81 relativ hoch. Bei MSCI World gefällt mir die starke Gewichtung der USA mit zirka 50% und Grossbritannien mit zirka 10% nicht unbedingt.
In einem weiteren Eintrag werde ich vermehrt über die Korrelationen und Portfoliotheorie schreiben…
[1] Volatilitäts-Kompass